如图，两个等腰直角△ABC和△CDE中，∠ACB＝∠DCE＝90°.

0 返回出卷网首页

1. 如图，两个等腰直角△ABC和△CDE中，∠ACB＝∠DCE＝90°.

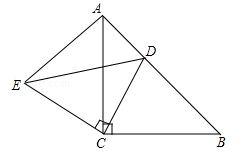
(1) 观察猜想如图1，点E在BC上，线段AE与BD的数量关系是_ ，位置关系是_.

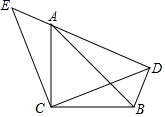
(2) 探究证明把△CDE绕直角顶点C旋转到图2的位置，（1）中的结论还成立吗？说明理由；

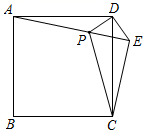
(3) 拓展延伸：把△CDE绕点C在平面内自由旋转，若AC＝BC＝13，DE＝10，当A、E、D三点在同一条直线上时，请直接写出AD的长.

【考点】

勾股定理; 等腰直角三角形; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ 和 $\text{[math]}$ 都是等腰直角三角形， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上一点.

(1) 求证： $\text{[math]}$ .

(2) 已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长度.

综合题普通

2. 如图，△ACB和△ECD都是等腰直角三角形，CA＝CB，CE＝CD，△ACB的顶点A在△ECD的斜边DE上.

(1) 求证：∠ADB＝90°；

(2) 若AE＝2，AD＝4，求AC.

综合题普通

3. 小平所在的学习小组发现，车辆转弯时，能否顺利通过直角弯道的标准是，车辆是否可以行驶到和路的边界夹角是45°的位置（如图1中②的位置）．例如，图2是某巷子的俯视图，巷子路面宽4m，转弯处为直角，车辆的车身为矩形ABCD，CD与DE、CE的夹角都是45°时，连接EF，交CD于点G，若GF的长度至少能达到车身宽度，即车辆能通过．

(1) 小平认为长8m，宽3m的消防车不能通过该直角转弯，请你帮他说明理由；

(2) 小平提出将拐弯处改为圆弧（ $\text{[math]}$ 和 $\text{[math]}$ 是以O为圆心，分别以OM和ON为半径的弧），长8m，宽3m的消防车就可以通过该弯道了，具体的方案如图3，其中OM⊥OM′，你能帮小平算出，ON至少为多少时，这种消防车可以通过该巷子？

综合题困难