如图，已知二次函数的图象经过点，，．

0 返回出卷网首页

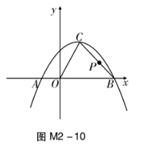
1. 如图，已知二次函数的图象经过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求抛物线的解析式；

(2) 求 $\text{[math]}$ 的面积；

(3) 若P是抛物线上一点且 $\text{[math]}$ 这样的P有几个？请直接写出它们的坐标．

【考点】

待定系数法求二次函数解析式; 三角形的面积;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知抛物线对称轴是直线x=2，且图象经过点（2，1）和点（1，0）．

(1) 求抛物线解析式；

(2) 若抛物线与x轴交于点A，点B，与y轴交于点C，求△ABC的面积．

综合题普通

2. 已知：如图M2-10，抛物线y=ax²+x+c与x轴交于点A(-1，0），B(3，0）．

(1) 试确定该抛物线的函数表达式；

(2) 已知点C是该抛物线的顶点，求△OBC的面积；

(3) 若点P是线段BC上的一动点，求OP的最小值．

综合题普通

3. 如图，顶点为 $\text{[math]}$ 的抛物线与x轴交于A，B两点， $\text{[math]}$ ．

(1) 求抛物线的解析式；

(2) 若点Q在抛物线上，且 $\text{[math]}$ 的面积为12，求点Q的坐标．

综合题普通