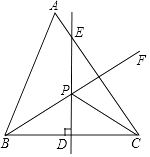
1.
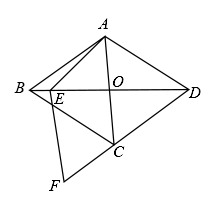
如图,菱形 的边长为10,
的边长为10,  , 对角线
, 对角线 相交于点O,点E在对角线BD上,连接AE,作
相交于点O,点E在对角线BD上,连接AE,作 且边EF与直线DC相交于点F.
且边EF与直线DC相交于点F.
(1)
求菱形 的面积;
(2)
求证
的面积;
(2)
求证 .
.
【考点】
三角形内角和定理;
线段垂直平分线的性质;
菱形的性质;
能力提升