1.
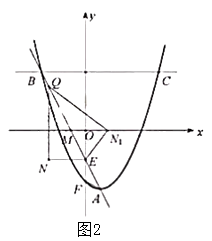
如图,二次函数 与
与 轴交于
轴交于 (0,0),
(0,0), (4,0)两点,顶点为
(4,0)两点,顶点为 , 连接
, 连接 、
、 , 若点
, 若点 是线段
是线段 上一动点,连接
上一动点,连接 , 将
, 将 沿
沿 折叠后,点
折叠后,点 落在点
落在点 的位置,线段
的位置,线段 与
与 轴交于点
轴交于点 , 且点
, 且点 与
与 、
、 点不重合.
点不重合.
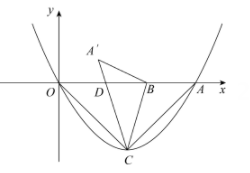
(1)
求二次函数的表达式;
(2)
①求证: ;
(3)
当
;
(3)
当 时,求直线
时,求直线 与二次函数的交点横坐标.
与二次函数的交点横坐标.
②求;
【考点】
待定系数法求二次函数解析式;
翻折变换(折叠问题);
相似三角形的判定与性质;
二次函数与一次函数的综合应用;
坐标系中的两点距离公式;
能力提升