为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长12m）和21m长的篱笆墙，围成I、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：

0 返回出卷网首页

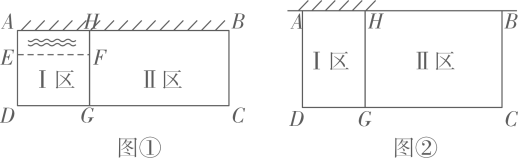
1. 为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长12m）和21m长的篱笆墙，围成I、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：

(1) 方案一：如图①，全部利用围墙的长度，但要在I区中留一个宽度AE=1m的水池，且需保证总种植面积为32m² ，试分别确定CG、DG的长；

(2) 方案二：如图②，使围成的两块矩形总种植面积最大，请问BC应设计为多长？此时最大面积为多少？

【考点】

一元一次方程的实际应用-几何问题; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 太原的五月是月季的狂欢，滨河路上月季花扮靓道路两侧，形成了“绿染龙城，花满并州”的景观效果．市林业局将如图所示的一块长80米，宽40米的矩形空地分成五块小矩形区域，建成月季花种植基地．一块正方形区域为育苗区，一块矩形区域为存储区，其它区域分别种植风花月季，藤本月季和树桩月季．已知存储区的一边与育苗区的宽相等，另一边长为20米，风花月季、藤本月季和树桩月季每年每平方米的产值分别为200元、300元和400元．

(1) 如果风花月季与藤本月季每年的产值相等，求育苗区的边长；

(2) 如果风花月季种植面积与育苗区面积的差不超过2120平方米，求这三种月季花每年总产值的最大值．

综合题普通

2. 已知C为线段AB上一点，关于x的两个方程 $\text{[math]}$ （x+1）＝m与 $\text{[math]}$ （x+m）＝m的解分别为线段AC ， BC的长，

(1) 当m＝2时，求线段AB的长；

(2) 若C为线段AB的三等分点，求m的值．

综合题普通

3. 如图，某小区进行项目改造：在一块长 $\text{[math]}$ 、宽 $\text{[math]}$ 的长方形场地 $\text{[math]}$ 上，分别设计与 $\text{[math]}$ ， $\text{[math]}$ 平行的横向和纵向通道，其余部分铺上草皮，如果通道的宽度相等，六块草坪的形状、大小相同，其中一块草坪的两边 $\text{[math]}$ ；

(1) 求通道的宽是多少m?

(2) 如果通道造价为40元/ $\text{[math]}$ ，草坪造价为100元/ $\text{[math]}$ ，只考虑通道和草坪的造价，不考虑人工等其他费用的前提下，完成该项目需要多少钱?

综合题普通