0 返回出卷网首页
1. 已知： ．

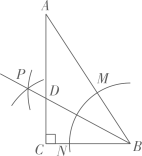
(1) 尺规作图：用直尺和圆规作出内切圆的圆心O；（只保留作图痕迹，不写作法和证明）
(2) 如果的周长为14 ， 内切圆的半径为1.3 ， 求的面积．
【考点】
三角形的面积; 尺规作图-作角的平分线;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．

问题引入：

(1) 如图①，当点D是BC边上的中点时，S△ABD：S△ABC=；当点D是BC边上任意一点时，S△ABD：S△ABC=（用图中已有线段表示）．
(2) 如图②，在△ABC中，O点是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．
(3) 如图③，O是线段AD上一点（不与点A、D重合），连结BO并延长交AC于点F，连结CO并延长交AB于点E，试猜想 + + 的值，并说明理由．
综合题 普通
2. 如图，点D双曲线上，AD垂直x轴，垂足为A，点C在AD上，CB平行于x轴交曲线于点B，直线AB与y轴交于点F，已知AC：AD=1：3，点C的坐标为（2，2）．

(1) 求该双曲线的解析式；
(2) 求△OFA的面积．
综合题 普通
3. 探究证明：

(1) 如图1，在△ABC中，AB=AC，点E是BC上的一个动点，EG⊥AB，EF⊥AC，CD⊥AB，点G，F，D分别是垂足．求证：CD=EG+EF；

猜想探究：
(2) 如图2，在△ABC中，AB=AC，点E是BC的延长线上的一个动点，EG⊥AB于G，EF⊥AC交AC延长线于F，CD⊥AB于D，直接猜想CD、EG、EF之间的关系为；
(3) 如图3，边长为10的正方形ABCD的对角线相交于点O、H在BD上，且BH=BC，连接CH，点E是CH上一点，EF⊥BD于点F，EG⊥BC于点G，则EF+EG=．
综合题 普通