1.
我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题.

(1)
如图一,在等腰 中,
中, ,
,  边上有一点D,过点D作
边上有一点D,过点D作 于E,
于E, 于F,过点C作
于F,过点C作 于G.利用面积证明:
于G.利用面积证明: .
(2)
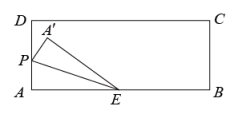
如图二,将矩形
.
(2)
如图二,将矩形 沿着
沿着 折叠,使点A与点C重合,点B落在
折叠,使点A与点C重合,点B落在 处,点G为折痕
处,点G为折痕 上一点,过点G作
上一点,过点G作 于M,
于M, 于N.若
于N.若 ,
,  , 求
, 求 的长.
(3)
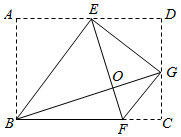
如图三,在四边形
的长.
(3)
如图三,在四边形 中,E为线段
中,E为线段 上的一点,
上的一点, ,
,  , 连接
, 连接 , 且
, 且 ,
,  ,
,  ,
,  , 求
, 求 的长.
的长.
【考点】
勾股定理;
翻折变换(折叠问题);
四边形的综合;