已知二次函数y＝ax2+bx+c的图象过点A（﹣1，0），B（3，0），且与y轴交于点C（0，﹣3）.

0 返回出卷网首页

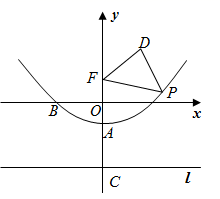
1. 已知二次函数y＝ax²+bx+c的图象过点A（﹣1，0），B（3，0），且与y轴交于点C（0，﹣3）.

(1) 求此二次函数的表达式及图象顶点D的坐标；

(2) 在此抛物线的对称轴上是否存在点E，使△ACE为Rt△，若存在，试求点E的坐标，若不存在，请说明理由；

(3) 在平面直角坐标系中，存在点P，满足PA⊥PD，求线段PB的最小值.

【考点】

待定系数法求二次函数解析式; 勾股定理; 点与圆的位置关系; 坐标系中的两点距离公式;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在直角坐标系中，已知直线y=﹣ $\text{[math]}$ x+4与y轴交于A点，与x轴交于B点，C点的坐标为（﹣2，0）．

(1) 求证：直线AB⊥AC；

(2) 求经过A，B，C三点的抛物线l的解析式和对称轴；

(3) 在直线AB上方的抛物线l上，是否存在一点P，使直线AB平分∠PBC？

若存在，请求出P点的坐标；若不存在，请说明理由．

综合题困难

2. 如图，抛物线的顶点为 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 轴上的一个定点.点 $\text{[math]}$ 是抛物线上一动点.

(1) 求这条抛物线的函数解析式；

(2) 已知直线 $\text{[math]}$ 是过点 $\text{[math]}$ 且垂直于 $\text{[math]}$ 轴的定直线，若点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离为 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(3) 已知坐标平面内一点 $\text{[math]}$ ，求 $\text{[math]}$ 周长的最小值，并求出此时 $\text{[math]}$ 点坐标.

综合题困难

3. 如图，已知抛物线 $\text{[math]}$ 交x轴于点 $\text{[math]}$ 和点 $\text{[math]}$ ，交y轴于点C，点D与点C关于抛物线的对称轴对称．

(1) 求该抛物线的表达式，并求出点D的坐标；

(2) 若点E为该抛物线上的点，点F为直线 $\text{[math]}$ 上的点，若 $\text{[math]}$ 轴，且 $\text{[math]}$ （点E在点F左侧），求点E的坐标；

(3) 若点P是该抛物线对称轴上的一个动点，是否存在点P，使得 $\text{[math]}$ 为直角三角形？若不存在，请说明理由；若存在，直接写出点P坐标．

综合题普通