1.
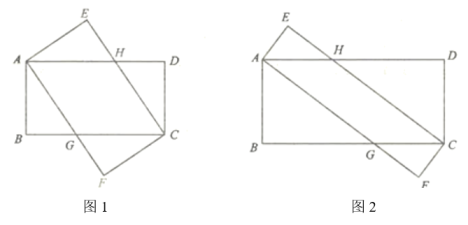
【探索发现】在一次折纸活动中,小亮同学选用了常见的A4纸,如图①,矩形 为它的示意图.他查找了A4纸的相关资料,根据资料显示得出图①中
为它的示意图.他查找了A4纸的相关资料,根据资料显示得出图①中 . 他先将A4纸沿过点A的直线折叠,使点B落在
. 他先将A4纸沿过点A的直线折叠,使点B落在 上,点B的对应点为点E,折痕为
上,点B的对应点为点E,折痕为 ;再沿过点F的直线折叠,使点C落在
;再沿过点F的直线折叠,使点C落在 上,点C的对应点为点H,折痕为
上,点C的对应点为点H,折痕为 ;然后连结
;然后连结 , 沿
, 沿 所在的直线再次折叠,发现点D与点F重合,进而猜想
所在的直线再次折叠,发现点D与点F重合,进而猜想 .
.
(1)
【问题解决】
(2)
【结论应用】
(3)
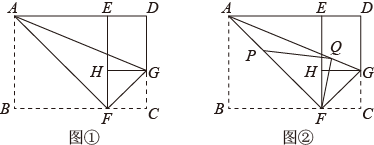
在图①的条件下,点P在线段 上,且
上,且 , 点Q在线段
, 点Q在线段 上,连结
上,连结 、
、 , 如图②,设
, 如图②,设 , 则
, 则 的最小值为.(用含a的代数式表示)
的最小值为.(用含a的代数式表示)
小亮对上面的猜想进行了证明,下面是部分证明过程:
证明:四边形是矩形,
∴ .
由折叠可知, ,
.
∴ .
∴ .
请你补全余下的证明过程.
的度数为度,
的值为;
【考点】
矩形的性质;
四边形的综合;
能力提升
真题演练