如图，AB是⊙O的直径，E为⊙O上的一点，∠ABE的平分线交⊙O于点C，过点C的直线交BA的延长线于点P，交BE的延长线于点D.且∠PCA＝∠CBD.

0 返回出卷网首页

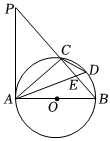
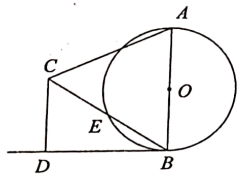
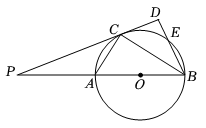
1. 如图，AB是⊙O的直径，E为⊙O上的一点，∠ABE的平分线交⊙O于点C，过点C的直线交BA的延长线于点P，交BE的延长线于点D.且∠PCA＝∠CBD.

(1) 求证：PC为⊙O的切线；

(2) 若PC＝ $\text{[math]}$ BO，PB＝12，求⊙O的半径及BE的长.

【考点】

等腰三角形的性质; 圆周角定理; 切线的判定; 两条直线被一组平行线所截，所得的对应线段成比例; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；

(2) 延长 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的半径．

综合题普通

2. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的直线交OP于点C，且∠CBP＝∠ADB.

(1) 求证：BC为⊙O的切线；

(2) 若OA＝2，AB＝ $\text{[math]}$ ，求线段BP的长.

综合题普通

3. 如图，在等腰 $\text{[math]}$ 中， $\text{[math]}$ 以 $\text{[math]}$ 为直径作⊙O交 $\text{[math]}$ 于E，过点B作 $\text{[math]}$ ，过点C作 $\text{[math]}$ 于D.

(1) 求证： $\text{[math]}$ 是⊙O的切线；

(2) 若 $\text{[math]}$ ，求⊙O的直径.

综合题困难