如图1，△ABC是等腰直角三角形，AC=BC=4，∠C=90°，M，N分别是边AC，BC上的点，以CM，CN为邻边作矩形PMCN，交AB于E，F．设CM=a，CN=b，若ab=8．

0 返回出卷网首页

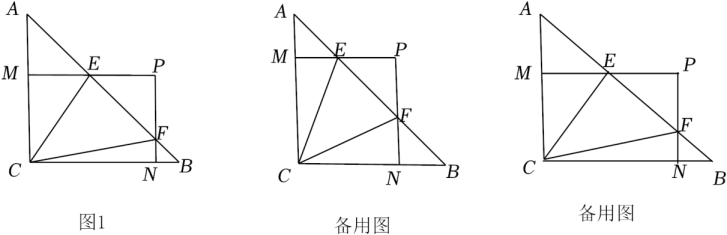
1. 如图1，△ABC是等腰直角三角形，AC=BC=4，∠C=90°，M，N分别是边AC，BC上的点，以CM，CN为邻边作矩形PMCN，交AB于E，F．设CM=a，CN=b，若ab=8．

(1) 判断由线段AE，EF，BF组成的三角形的形状，并说明理由；

(2) ①当a=b时，求∠ECF的度数；

②当a≠b时，①中的结论是否成立？并说明理由．

【考点】

勾股定理; 等腰直角三角形; 三角形全等的判定-SSS; 四边形的综合;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，∠ACB=90°，AC=BC，AB为水平边，D为AB边上一点.

(1) 只用圆规在B的正上方作一点E，使BE=AD（说明作法，不需要证明）；

(2) 在（1）的条件下，连接DE，若AC= $\text{[math]}$ ，AD=3，求DE的长度.

综合题普通

2. 小平所在的学习小组发现，车辆转弯时，能否顺利通过直角弯道的标准是，车辆是否可以行驶到和路的边界夹角是45°的位置（如图1中②的位置）．例如，图2是某巷子的俯视图，巷子路面宽4m，转弯处为直角，车辆的车身为矩形ABCD，CD与DE、CE的夹角都是45°时，连接EF，交CD于点G，若GF的长度至少能达到车身宽度，即车辆能通过．

(1) 小平认为长8m，宽3m的消防车不能通过该直角转弯，请你帮他说明理由；

(2) 小平提出将拐弯处改为圆弧（ $\text{[math]}$ 和 $\text{[math]}$ 是以O为圆心，分别以OM和ON为半径的弧），长8m，宽3m的消防车就可以通过该弯道了，具体的方案如图3，其中OM⊥OM′，你能帮小平算出，ON至少为多少时，这种消防车可以通过该巷子？

综合题困难

3. 如图1，用平面去截一个正方体，得到了一个如图2的几何体，通过测量得到 $\text{[math]}$ ， $\text{[math]}$ .

（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

(1) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的长.

综合题普通