0 返回出卷网首页
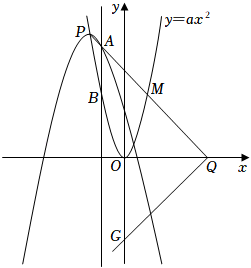
1. 如图，在平面直角坐标系xOy中，抛物线E：y＝﹣（x﹣m）2+2m2（m＜0）的顶点P在抛物线F：y＝ax2上，直线x＝t与抛物线E，F分别交于点A，B．

(1) 求a的值；
(2) 将A，B的纵坐标分别记为yA，yB，设s＝yA﹣yB，若s的最大值为4，则m的值是多少？
(3) Q是x轴的正半轴上一点，且PQ的中点M恰好在抛物线F上．试探究：此时无论m为何负值，在y轴的负半轴上是否存在定点G，使∠PQG总为直角？若存在，请求出点G的坐标；若不存在，请说明理由．
【考点】
待定系数法求二次函数解析式; 相似三角形的判定与性质; 二次函数的实际应用-几何问题;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 如图，抛物线y＝ax2＋bx＋c交x轴于A(-1，0)，B两点，交y轴于点C(0，3)，顶点D的横坐标为1．

(1) 求抛物线的解析式；
(2) 在y轴的负半轴上是否存在点P使∠APB＋∠ACB＝180°．若存在，求出点P的坐标，若不存在，请说明理由；
(3) 过点C作直线l与y轴垂直，与抛物线的另一个交点为E，连接AD，AE，DE，在直线l下方的抛物线上是否存在一点M，过点M作MF⊥l，垂足为F，使以M，F，E三点为顶点的三角形与ΔADE相似？若存在，请求出M点的坐标，若不存在，请说明理由．
综合题 困难
2. 如图①，直线l经过点（4，0）且平行于y轴，二次函数y＝ax2﹣2ax+c（a、c是常数，a＜0）的图象经过点M(﹣1，1)，交直线l于点N，图象的顶点为D，它的对称轴与x轴交于点C，直线DM、DN分别与x轴相交于A、B两点.

(1) 当a＝﹣1时，求点N的坐标及 的值；
(2) 随着a的变化， 的值是否发生变化？请说明理由；
(3) 如图②，E是x轴上位于点B右侧的点，BC＝2BE，DE交抛物线于点F.若FB＝FE，求此时的二次函数表达式.
 
综合题 困难
3. 如图，在平面直角坐标系中，抛物线y=ax2+bx+c与x轴相交于A、B两点（A在B的左侧），与y轴相交于点C（0，3)，且OA=3，OB=1，抛物线的顶点为D。

(1) 求A、B两点的坐标。
(2) 求抛物线的表达式。
(3) 过点D作直线DE∥y轴，交x轴于点E，点P是抛物线上B，D两点间的一个动点（点P不与B、D两点重合），PA、BP与直线DE分别相交于点F、G，当点P运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由。
综合题 困难