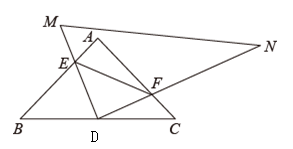
与探究，如图，△ABC为等腰直角三角形，点D为斜边BC的中点，且，把另一个直角三角形的直角顶点放在点D处，两条直角边DM，DN分别交AB，AC于点E，F．把Rt△DMN绕点D转动，保持点E，F分别在线段AB，AC上（不与点A，B，C重合）．

0 返回出卷网首页

1. 与探究，如图，△ABC为等腰直角三角形，点D为斜边BC的中点，且 $\text{[math]}$ ，把另一个直角三角形的直角顶点放在点D处，两条直角边DM，DN分别交AB，AC于点E，F．把Rt△DMN绕点D转动，保持点E，F分别在线段AB，AC上（不与点A，B，C重合）．

(1) 请你判断DE与DF之间的数量关系并说明理由．

(2) 求四边形DEAF的面积．

(3) 求点E、F到线段BC的距离之和．

【考点】

旋转的性质; 等腰直角三角形; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图1)，且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，现将三角板EFG绕O点顺时针旋转，旋转角 $\text{[math]}$ 满足条件 $\text{[math]}$ 四边形CHGK是旋转过程中两三角板的重叠部分(如图2).

(1) 在上述旋转过程中，BH与CK有怎样的数量关系？证明你的结论；

(2) 在上述旋转过程中，两个直角三角形的重叠部分面积是否会发生改变？证明你的结论.

综合题普通

2. 旋转的性质:

(1) 对应点到旋转中心的距离;

(2) 任意一组对应点与旋转中心的连线所成的角等于;

(3) 旋转前、后的图形.

综合题普通

3. 如图1，把△ABC沿直线BC平移线段BC的长度，得到△ECD；如图2，以BC为轴，把△ABC沿BC翻折180°，可以得到△DBC；如图3，以点A为中心，把△ABC旋转180°，可以得到△AED ．像这样，其中一个三角形是由另一个三角形按平移、翻折、旋转等方法得到的，这种只改变位置，不改变形状、大小的图形变换，叫做三角形的全等变换．回答下列问题：

(1) 在图4中，可以使△ABE通过平移、翻折、旋转中的哪一种方法得到△ADF？

(2) 图中线段BE与DF相等吗？为什么？

综合题普通