1.
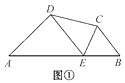
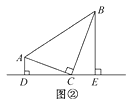
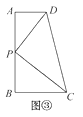
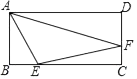
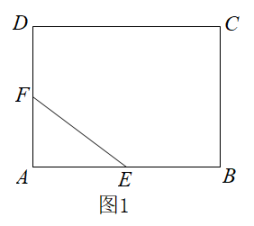
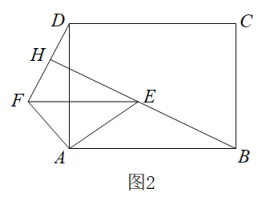
如图,将① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ 中的一个作为条件,另一个作为结论,组成一个真命题.
中的一个作为条件,另一个作为结论,组成一个真命题.
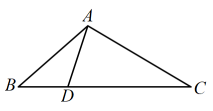
(1)
条件是,结论是;(注:填序号)
(2)
写出你的证明过程.
【考点】
相似三角形的判定与性质;
能力提升
真题演练