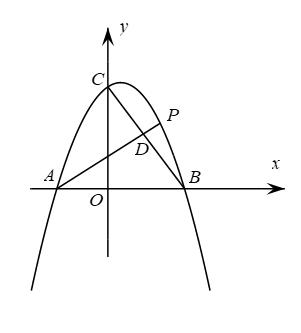
如图，抛物线y=ax2﹣ x﹣2（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．

0 返回出卷网首页

1. 如图，抛物线y=ax²﹣ $\text{[math]}$ x﹣2（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．

(1) 求抛物线的解析式；

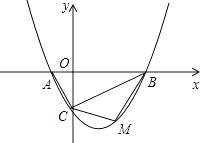
(2) 试探究△ABC的外接圆的圆心位置，并求出圆心坐标；

(3) 若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．

【考点】

二次函数图象与坐标轴的交点问题; 三角形的外接圆与外心; 相似三角形的判定与性质; 二次函数与一次函数的综合应用; 直角三角形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在平面直角坐标系中，抛物线y=ax²+6x+c（a≠0）交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，﹣5），点B的坐标为（1，0）．

(1) 求此抛物线的解析式及定点坐标；

(2) 过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与⊙C的位置关系，并说明理由；

(3) 在抛物线上是否存在一点P，使△ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

综合题困难

2. 如图，抛物线 $\text{[math]}$ 与坐标轴分别交于A，B，C三点，P是第一象限内抛物线上的一点且横坐标为m．

(1) A，B，C三点的坐标为，，；

(2) 连接 $\text{[math]}$ ，交线段 $\text{[math]}$ 于点D，

①当 $\text{[math]}$ 与x轴平行时，求 $\text{[math]}$ 的值；

②当 $\text{[math]}$ 与x轴不平行时，求 $\text{[math]}$ 的最大值；

(3) 连接 $\text{[math]}$ ，是否存在点P，使得 $\text{[math]}$ ，若存在，求m的值，若不存在，请说明理由．

综合题困难

3. 在平面直角坐标系 $\text{[math]}$ 中，已知抛物线 $\text{[math]}$ ．

(1) 求抛物线顶点 $\text{[math]}$ 的坐标；（用含 $\text{[math]}$ 的代数式表示）

(2) 抛物线与 $\text{[math]}$ 轴只有一个公共点，经过点 $\text{[math]}$ 的直线与抛物线交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．

①判断 $\text{[math]}$ 的形状，并说明理由；

②已知点 $\text{[math]}$ ，点 $\text{[math]}$ ，设 $\text{[math]}$ 的外心为点 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上时，求点 $\text{[math]}$ 的纵坐标 $\text{[math]}$ 的取值范围．

综合题困难