1.
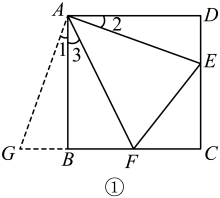
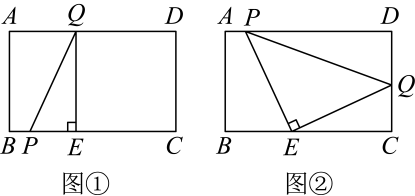
如图①.在矩形 .
.  , 点
, 点 在边
在边 上,且
上,且 . 动点
. 动点 从点
从点 出发,沿折线
出发,沿折线 以每秒
以每秒 个单位长度的速度运动,作
个单位长度的速度运动,作 ,
,  交边
交边 或边
或边 于点
于点 , 连续
, 连续 . 当点
. 当点 与点
与点 重合时,点
重合时,点 停止运动.设点
停止运动.设点 的运动时间为
的运动时间为 秒.(
秒.( )
)
(1)
当点 和点
和点 重合时,线段
重合时,线段 的长为;
(2)
当点
的长为;
(2)
当点 和点
和点 重合时,求
重合时,求 ;
(3)
当点
;
(3)
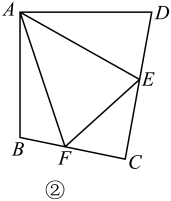
当点 在边
在边 上运动时,
上运动时, 的形状始终是等腰直角三角形.如图②.请说明理由;
(4)
作点
的形状始终是等腰直角三角形.如图②.请说明理由;
(4)
作点 关于直线
关于直线 的对称点
的对称点 , 连接
, 连接 、
、 , 当四边形
, 当四边形 和矩形
和矩形 重叠部分图形为轴对称四边形时,直接写出
重叠部分图形为轴对称四边形时,直接写出 的取值范围.
的取值范围.
【考点】
三角形全等及其性质;
三角形全等的判定;
勾股定理;
矩形的判定与性质;
正方形的性质;
相似三角形的判定与性质;
能力提升