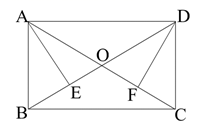
1.
已知:正方形 中,点E,M分别在边
中,点E,M分别在边 ,
,  上.
上.

(1)
如图1, , 垂足为点G,求证:
, 垂足为点G,求证: ;
(2)
如图2,点F,N分别在边
;
(2)
如图2,点F,N分别在边 ,
,  上,若
上,若 , 请判断
, 请判断 和
和 的大小关系,并说明理由.
的大小关系,并说明理由.
【考点】
余角、补角及其性质;
垂线的概念;
矩形的判定与性质;
正方形的性质;
三角形全等的判定-AAS;