“先天下之忧而忧，后天下之乐而乐”这是《岳阳楼记》中的一句千古名言，也是岳阳精神的真实写照，这句话具有鲜明的对称美．如果一个凸四边形沿着它的一条对角线对折后能完全重合，我们就把这个四边形称为“忧乐四边形”．如图1，凸四边形沿对角线对折后完全重合，四边形是以直线为对称轴的“忧乐四边形”．

0 返回出卷网首页

1. “先天下之忧而忧，后天下之乐而乐”这是《岳阳楼记》中的一句千古名言，也是岳阳精神的真实写照，这句话具有鲜明的对称美．如果一个凸四边形沿着它的一条对角线对折后能完全重合，我们就把这个四边形称为“忧乐四边形”．如图1，凸四边形 $\text{[math]}$ 沿对角线 $\text{[math]}$ 对折后完全重合，四边形 $\text{[math]}$ 是以直线 $\text{[math]}$ 为对称轴的“忧乐四边形”．

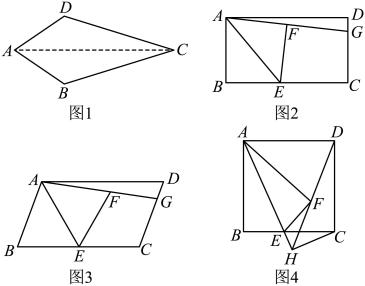
(1) 下列四边形一定是“忧乐四边形”的有（填序号）

①平行四边形；②长方形；③正方形；④菱形；⑤梯形

(2) 在四边形 $\text{[math]}$ 中，点E是 $\text{[math]}$ 边上的中点，四边形 $\text{[math]}$ 是以直线 $\text{[math]}$ 为对称轴的“忧乐四边形”（点F在四边形 $\text{[math]}$ 内部），连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点G ．

①如图2，若四边形 $\text{[math]}$ 是矩形，求证：四边形 $\text{[math]}$ 是“忧乐四边形”．

②如图3，若四边形 $\text{[math]}$ 是平行四边形，①中的结论是否仍然成立，请说明理由．

(3) 如图4，四边形 $\text{[math]}$ 是正方形，且点E为线段 $\text{[math]}$ 上的动点（不与B、C重合），四边形 $\text{[math]}$ 是以直线 $\text{[math]}$ 为对称轴的“忧乐四边形”（点F在正方形 $\text{[math]}$ 内部），连接 $\text{[math]}$ 并延长，与 $\text{[math]}$ 的延长线交于点H ，连接 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 三条线段之间的数量关系．

【考点】

三角形全等的判定; 勾股定理; 平行四边形的性质; 矩形的性质; 翻折变换（折叠问题）; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难