1.
在 中,
中, ,
,  , 给出如下定义:作直线
, 给出如下定义:作直线 分别交
分别交 ,
,  边于点
边于点 ,
,  , 点
, 点 关于直线
关于直线 的对称点为
的对称点为 , 则称
, 则称 为等腰直角
为等腰直角 关于直线
关于直线 的“直角对称点”
的“直角对称点” 点
点 可与点
可与点 重合,点
重合,点 可与点
可与点 重合
重合
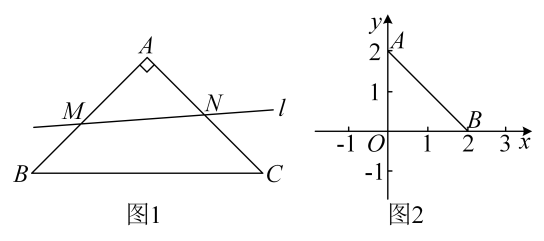
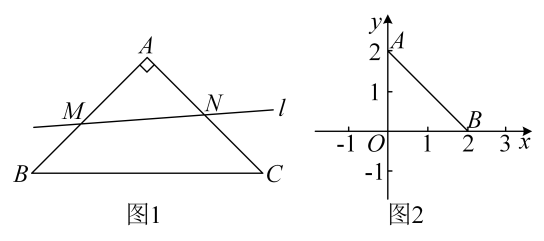
(1)
在平面直角坐标系 中,点
中,点 ,
,  , 直线
, 直线 :
: ,
,  为等腰直角
为等腰直角 关于直线
关于直线 的“直角对称点”.
的“直角对称点”.
 当
当 时,写出点
时,写出点 的坐标;
的坐标;
 连接
连接 , 求
, 求 长度的取值范围;
(2)
长度的取值范围;
(2)
 的半径为
的半径为 , 点
, 点 是
是 上一点,以点
上一点,以点 为直角顶点作等腰直角
为直角顶点作等腰直角 , 其中
, 其中 , 直线
, 直线 与
与 、
、 分别交于
分别交于 、
、 两点,同时
两点,同时 为等腰直角
为等腰直角 关于直线
关于直线 的“直角对称点”,连接
的“直角对称点”,连接 , 当点
, 当点 在
在 上运动时,直接写出
上运动时,直接写出 长度的最大值与最小值.
长度的最大值与最小值.
【考点】
三角形三边关系;
勾股定理;
关于坐标轴对称的点的坐标特征;
等腰直角三角形;
能力提升



