1.
如图,在边长为 的正方形
的正方形 中,点
中,点 ,
,  分别为
分别为 ,
,  边上的点,将正方形
边上的点,将正方形 沿
沿 翻折,点
翻折,点 的对应点为
的对应点为 , 点
, 点 恰好落在
恰好落在 边的点
边的点 处.
处.


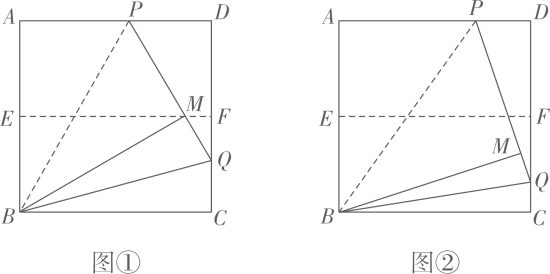
(1)
【问题解决】如图 , 连接
, 连接 , 则
, 则 与折痕
与折痕 的位置关系是 ,
的位置关系是 , 与
与 的数量关系是 ;
(2)
【问题探究】如图
的数量关系是 ;
(2)
【问题探究】如图 , 连接
, 连接 , 在翻折过程中,
, 在翻折过程中, 平分
平分 , 试探究
, 试探究 的面积是否为定值,若为定值,请求出
的面积是否为定值,若为定值,请求出 的面积;若不是定值,请说明理由;
(3)
【拓展延伸】若
的面积;若不是定值,请说明理由;
(3)
【拓展延伸】若 , 求出
, 求出 的最小值.
的最小值.
【考点】
勾股定理;
正方形的性质;
轴对称的应用-最短距离问题;
翻折变换(折叠问题);
三角形全等的判定-ASA;
能力提升