1.
我国古代数学家刘徽通过“割圆术”来估计圆周率 的值——“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,可以理解为当正多边形的边数越来越多时,该正多边形与它的外接圆越来越“接近”,这样就可以用正多边形的周长替代它的外接圆的周长,从而估算出圆周率
的值——“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,可以理解为当正多边形的边数越来越多时,该正多边形与它的外接圆越来越“接近”,这样就可以用正多边形的周长替代它的外接圆的周长,从而估算出圆周率 的值.
的值.
(1)
对于边长为 的正方形,其外接圆半径为,根据故事中的方法,用该正方形的周长
的正方形,其外接圆半径为,根据故事中的方法,用该正方形的周长 替代它的外接圆周长,利用公式
替代它的外接圆周长,利用公式 , 可以估算
, 可以估算 .
(2)
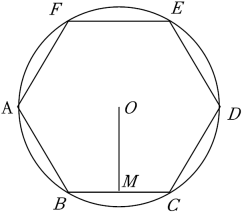
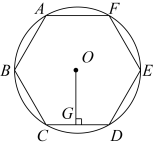
类比(1),当正多边形为正六边形时,估计
.
(2)
类比(1),当正多边形为正六边形时,估计 的值.
的值.
【考点】
勾股定理;
圆内接正多边形;