对于数轴上的点M，N，给出如下定义：若点M到点N的距离为d(d≥0)，则称d为点M到点N的追击值，记作d[MN].例如，在数轴上点M表示的数是6，点N表示的数是2，则点M到点N的追击值d[MN]=4.

0 返回出卷网首页

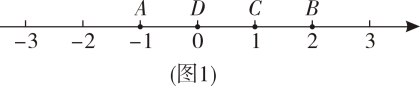
1. 对于数轴上的点M，N，给出如下定义：若点M到点N的距离为d(d≥0)，则称d为点M到点N的追击值，记作d[MN].例如，在数轴上点M表示的数是6，点N表示的数是2，则点M到点N的追击值d[MN]=4.

(1) 若点P，Q都在数轴上，点Р表示的数是1，且点Р到点Q的追击值d[PQ]=a，则点Q表示的数是(用含a的代数式表示).

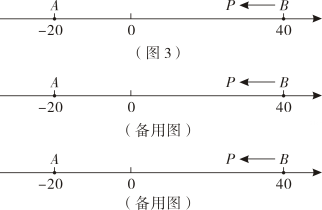
(2) 如图，若点F从数-1出发，点G从数2出发，沿着数轴正方向同时移动，点F的速度为每秒4个单位，点G的速度为每秒1个单位，设运动时间为t秒(t≥0).求当t为何值时，点F到点G的追击值d[FG]=2.

(3) 若点A从数1出发，点B从数4出发，点E从数6出发，沿着数轴正方向同时移动，点A的速度为每秒4个单位，点B的速度为每秒1个单位，点E的速度为每秒4个单位，设运动时间为t秒(t≥0)，请探究d[AB]与d[BE]之间的数量关系.

【考点】

数轴及有理数在数轴上的表示; 代数式求值; 一元一次方程的其他应用; 定义新运算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 阅读理解：

若 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为数轴上三点，若点 $\text{[math]}$ 到 $\text{[math]}$ 的距离是点 $\text{[math]}$ 到 $\text{[math]}$ 的距离 $\text{[math]}$ 倍，我们就称点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点．

例如，如图 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ 表示 $\text{[math]}$ 的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，那么点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点；又如，表示 $\text{[math]}$ 的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，那么点 $\text{[math]}$ 就不是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点，但点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点．

知识运用：如图 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为数轴上两点，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ．