如图，已知在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝16，D是AC上的一点，CD＝3，点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动，设点P的运动时间为t．连接AP．

0 返回出卷网首页

1. 如图，已知在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝16，D是AC上的一点，CD＝3，点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动，设点P的运动时间为t．连接AP．

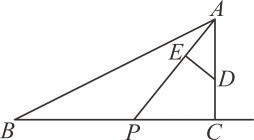
(1) 当t＝3秒时，求△BPA的面积；

(2) 若AP平分∠CAB，求t的值；

(3) 过点D作DE⊥AP于点E．在点P的运动过程中，当t为何值时，能使DE＝CD？

【考点】

角平分线的性质; 勾股定理的应用; 角平分线的判定; 三角形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图，在四边形ABDC中，∠D=∠B=90°，O为BD的中点，且AO平分∠BAC．

求证：

(1) CO平分∠ACD．

(2) AB+CD=AC．

解答题普通

2. 如图，BD和CD分别是 $\text{[math]}$ 两个外角的角平分线.

(1) 在图中分别作出点D到AB和AC的距离，判断并证明它们的等量关系；

(2) 请你再次判断点D是否在 $\text{[math]}$ 的角平分线上，说说你的理由.

解答题普通

如图，已知四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， E为CD边上的一点， $\text{[math]}$ ，动点P从点A出发，以每秒1个单位的速度沿着边AB向终点B运动，连接PE，设点P运动的时间为t秒.

(1) 求BE的长；

(2) 若△BPE为直角三角形，求t的值.

解答题困难