如图，△ABC是等边三角形，点D是边BC上的一点，以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．

0 返回出卷网首页

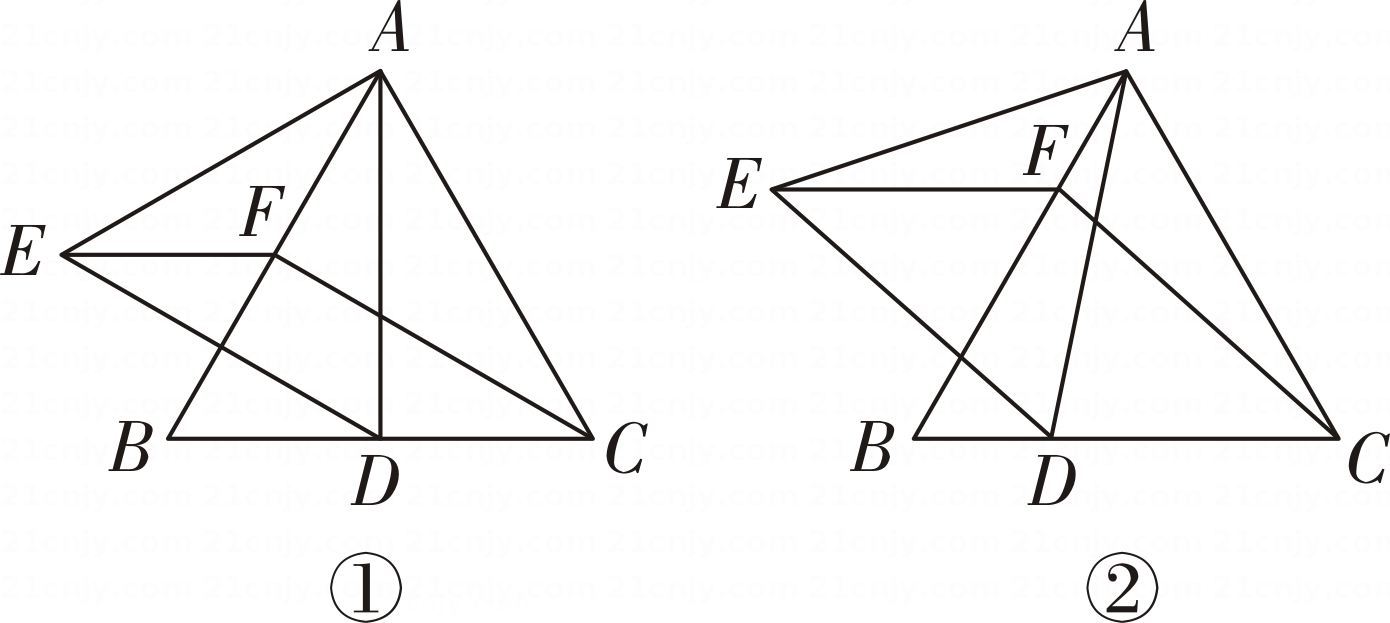
1. 如图，△ABC是等边三角形，点D是边BC上的一点，以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．

(1) 若点D是BC边的中点(如图①) ，求证：EF=CD．

(2) 在(1)的条件下直接写出△AEF和△ABC的面积比．

(3) 若点D是BC边上的任意一点(除B，C外，如图②) ，那么(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．

【考点】

三角形全等及其性质; 三角形全等的判定; 等边三角形的性质; 平行四边形的性质; 平行四边形的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图所示，在 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$

中点，连接 $\text{[math]}$ 并延长，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ．

(2) 连接 $\text{[math]}$ ，若 $\text{[math]}$ 平分 $\text{[math]}$ ，且当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长．

解答题普通

2. 如图，在平行四边形 $\text{[math]}$ 中，点 $\text{[math]}$ 、 $\text{[math]}$ 分别在边 $\text{[math]}$ 和 $\text{[math]}$ 上，且 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 求证： $\text{[math]}$ ．

解答题普通

3. 如图所示，已知▱ABCD，对角线AC、BD相交于点O，EF是过点O的任一直线，交AD于点E，交BC于F，试说明OE与OF之间的关系，并说明理由．

解答题普通