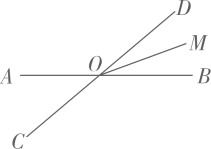
综合与探究【提出问题】小明在学习中遇到这样一个问题：如图1，，请作一个，使与互余（），即．【动手操作】小明是这样思考的：如图2所示，若射线在的内部，则，所以射线在的外部；然后通过构造直角，找到的余角，如图3所示；进而分析要使与互余，只需．因此，小明找到了解决问题的方法：过点O作射线的垂线，利用量角器作出的平分线，这样就得到与互余．请你帮助小明完成下列推理说明：

1. 综合与探究

【提出问题】小明在学习中遇到这样一个问题：如图1， $\text{[math]}$ ，请作一个 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 互余（ $\text{[math]}$ ），即 $\text{[math]}$ ．

【动手操作】小明是这样思考的：如图2所示，若射线 $\text{[math]}$ 在 $\text{[math]}$ 的内部，则 $\text{[math]}$ ，所以射线 $\text{[math]}$ 在 $\text{[math]}$ 的外部；然后通过构造直角 $\text{[math]}$ ，找到 $\text{[math]}$ 的余角，如图3所示；进而分析要使 $\text{[math]}$ 与 $\text{[math]}$ 互余，只需 $\text{[math]}$ ．

因此，小明找到了解决问题的方法：过点O作射线 $\text{[math]}$ 的垂线 $\text{[math]}$ ，利用量角器作出 $\text{[math]}$ 的平分线 $\text{[math]}$ ，这样就得到 $\text{[math]}$ 与 $\text{[math]}$ 互余．请你帮助小明完成下列推理说明：

(1) 已知：如图3， $\text{[math]}$ ，射线 $\text{[math]}$ 平分 $\text{[math]}$ ．请说明 $\text{[math]}$ 与 $\text{[math]}$ 互余．

解：理由：因为射线 $\text{[math]}$ 平分 $\text{[math]}$ （已知），

所以 $\text{[math]}$ （角平分线的定义），

由于 $\text{[math]}$ ，即 $\text{[math]}$ $\text{[math]}$ ，

所以 $\text{[math]}$ （），即 $\text{[math]}$ 与 $\text{[math]}$ 互余．

(2) 【类比操作】如图4，若 $\text{[math]}$ ，参考小明的画法，请在图4中作出一个 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 互补（ $\text{[math]}$ ），并直接写出 $\text{[math]}$ 的度数．

(3) 【拓展延伸】如图5，已知 $\text{[math]}$ ，若 $\text{[math]}$ 与 $\text{[math]}$ 互补，射线 $\text{[math]}$ 平分 $\text{[math]}$ ，射线 $\text{[math]}$ 平分 $\text{[math]}$ ．请根据题意，补全图形，并求 $\text{[math]}$ 的度数．