1.
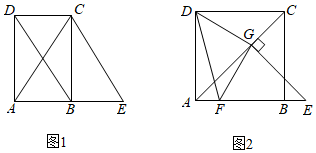
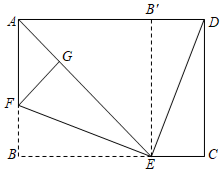
如图, 在长方形  中,
中,  , 点
, 点  从点
从点  出发, 以
出发, 以  的速度沿
的速度沿  向点
向点  运动, 设点
运动, 设点  的运动时间为
的运动时间为  秒.
秒.

(1)
当  为何值时,
为何值时,  与
与  全等.
(2)
当点
全等.
(2)
当点  从点
从点  开始运动, 同时, 点
开始运动, 同时, 点  从点
从点  出发, 以
出发, 以  的速度沿
的速度沿  向点
向点  运动, 是否存在这样的
运动, 是否存在这样的  值, 使得
值, 使得  与
与  全等? 若存在, 请求出
全等? 若存在, 请求出  的值; 若不存在, 请说明理由.
的值; 若不存在, 请说明理由.
【考点】
三角形全等及其性质;
三角形全等的判定;