1.
探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
在中,
,
, D是
边上一点,且
(n为正整数),E是
边上的动点,过点D作
的垂线交直线
于点F.
(1)
【初步感知】
(2)
【深入探究】
(3)
【拓展运用】
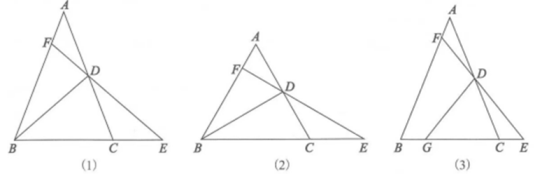
如图1,当时,兴趣小组探究得出结论:
, 请写出证明过程.
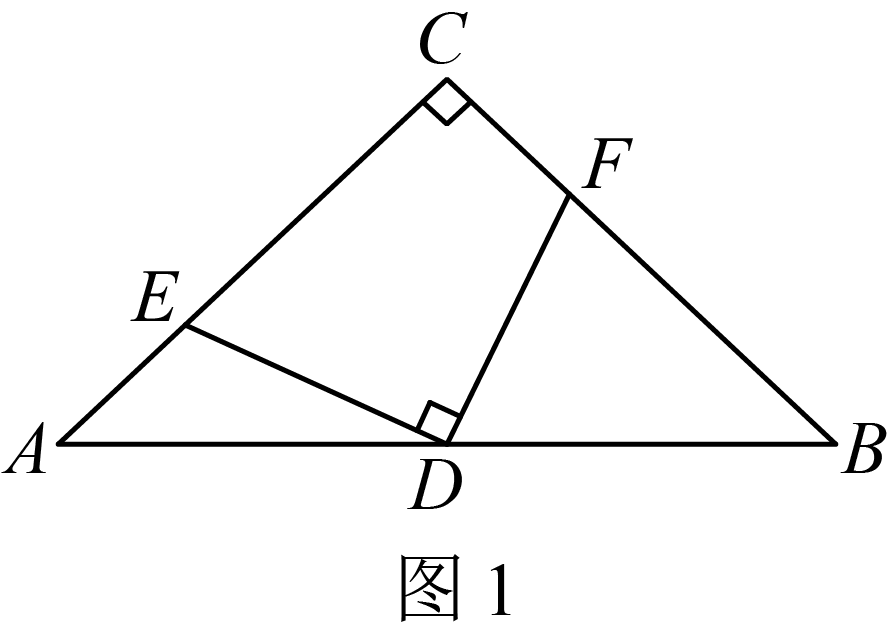
如图2,当 , 且点F在线段
上时,试探究线段
之间的数量关系,请写出结论并证明.
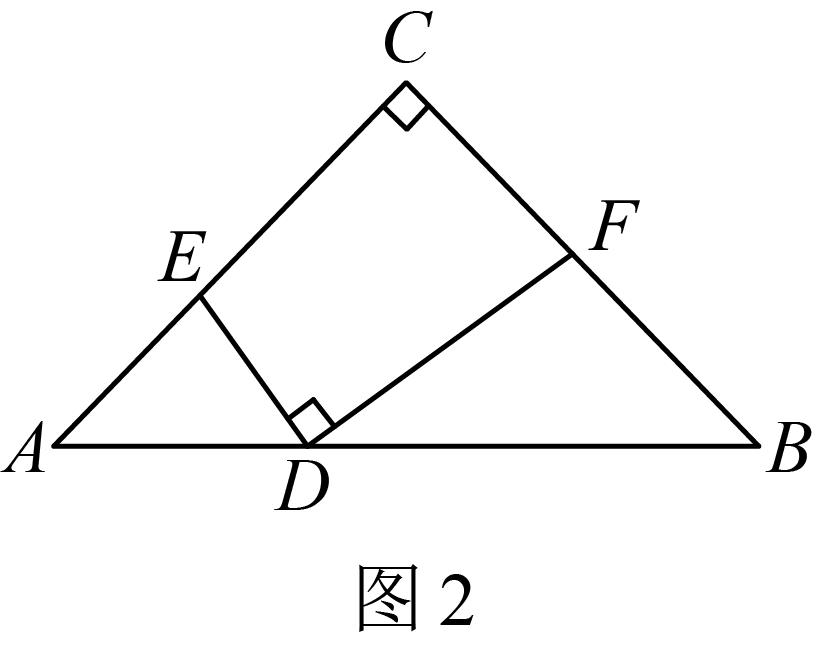
请通过类比、归纳、猜想,探究出线段之间数量关系的一般结论(直接写出结论,不必证明).
【考点】
相似三角形的判定与性质;
三角形全等的判定-ASA;
能力提升
真题演练