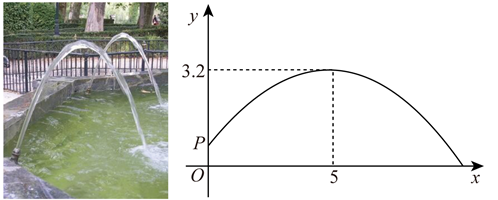
如图1为某公园的圆形喷水池，小玲学习了二次函数后，受到该图启发设计了一种新的喷水池，它的截面示意图如图2所示，为水池中心，喷头、之间的距离为米，喷射水柱呈抛物线形，水柱距水池中心处达到最高，高度为．水池中心处有一个圆柱形蓄水池，其高为米．

0 返回出卷网首页

1. 如图1为某公园的圆形喷水池，小玲学习了二次函数后，受到该图启发设计了一种新的喷水池，它的截面示意图如图2所示， $\text{[math]}$ 为水池中心，喷头 $\text{[math]}$ 、 $\text{[math]}$ 之间的距离为 $\text{[math]}$ 米，喷射水柱呈抛物线形，水柱距水池中心 $\text{[math]}$ 处达到最高，高度为 $\text{[math]}$ ．水池中心处有一个圆柱形蓄水池，其高 $\text{[math]}$ 为 $\text{[math]}$ 米．

(1) 在图2中，以点 $\text{[math]}$ 为坐标原点，水平方向为 $\text{[math]}$ 轴建立直角坐标系，并求右边这条抛物线的函数解析式．

(2) 如图3，拟在圆柱形蓄水池中心处建一喷水装置 $\text{[math]}$ ，从点 $\text{[math]}$ 向四周喷射抛物线形水柱且满足以下四个条件：不能碰到图2中的水柱；落水点 $\text{[math]}$ ， $\text{[math]}$ 的间距为 $\text{[math]}$ ；水柱的最高点与点 $\text{[math]}$ 的高度差为 $\text{[math]}$ ；从点 $\text{[math]}$ 向四周喷射与图2中形状相同的抛物线形水柱．

①在建立的坐标系中，求落水点 $\text{[math]}$ 的坐标；

②求出喷水装置 $\text{[math]}$ 的高度．

【考点】

二次函数的实际应用-喷水问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 某公园有一个水池，中心的可升降喷头垂直于地面，喷出的水柱形状呈抛物线。如图是喷水池喷水时的截面图，以喷水池中心O为原点，水平方向为x轴，1米为1个单位长度建立平面直角坐标系，设喷头A的坐标为(0，c)(c≥0)，抛物线的函数表达式中二次项系数为a.

(1) 当水柱都满足水平距离为4米时，达到最大高度为6米.

①若c=1，求第一象限内水柱的函数表达式(无需写取值范围).

②用含c的代数式表示a.

(2) 为了美化公园，对喷水设备进行改造，使a与c之间满足 $\text{[math]}$ ，且当水平距离为6米时，水柱达到最大高度，求改造后水柱达到的最大高度.

解答题普通

2. 为了有效地应对高楼火灾，某消防队进行消防技能比赛.如图，在一个废弃高楼距地面10m的点 $\text{[math]}$ 和15m的点 $\text{[math]}$ 处，各设置了一个火源，消防员来到火源正前方，水枪喷出的水流看作抛物线的一部分(水流出口与地面的距离忽略不计).第一次灭火时站在水平地面的点 $\text{[math]}$ 处，水流恰好到达点 $\text{[math]}$ 处，且水流的最大高度为16m，水流的最高点到高楼的水平距离为4m，建立如图所示的平面直角坐标系，水流的高度y(m)与到高楼的水平距离x(m)之间的函数关系式为 $\text{[math]}$ .

(1) 求消防员第一次灭火时水流所在抛物线的函数解析式；

(2) 待A处火熄灭后，消防员前进2m到点 $\text{[math]}$ 处进行第二次灭火.若两次灭火时水流所在抛物线的形状相同，请判断水流是否能到达点B处，并说明理由；

(3) 若消防员站在到高楼的水平距离为 $\text{[math]}$ 的地方，调整水枪，使喷出的水流形状发生变化，水流的最高点到高楼的水平距离始终是4m.当 $\text{[math]}$ 时，求水流到达墙面高度 $\text{[math]}$ 的取值范围.

解答题困难

3. 花坛水池中央有一喷泉，水管 $\text{[math]}$ ，水从喷头C喷出后呈抛物线状，先向上至最高点后落下，为增强欣赏效果，喷头C不定时自动升降，上下升降的范围是 $\text{[math]}$ ．建立如图所示的平面直角坐标系，水的落地点B距水池中央的水平距离为 $\text{[math]}$ ，水流所形成的抛物线L： $\text{[math]}$ 的最高点距离水面4m．

(1) 求a ， n的值以及抛物线的顶点坐标；

(2) 升降喷头C时，水流所形成的抛物线形状不变．某一时刻，身高1.65m的小丽同学，恰好站在距花坛中心水管2m的位置，则喷头C在升降过程中，水流是否会打湿小丽的头发？

解答题普通