1.
综合与实践:
综合与实践课上,老师让同学们以“正方形的折叠”为主题开展数学活动.
【操作判断】
操作一:
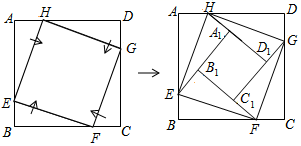
如图1,正方形纸片ABCD , 将沿过点A的直线折叠,使点B落在正方形ABCD的内部,得到折痕AE , 点B的对应点为M , 连接AM;将
沿过点A的直线折叠,使AD与AM重合,得到折痕AF , 将纸片展平,连接EF .

(1)
根据以上操作,易得点E , M , F三点共线,且① °;②线段EF , BE , DF之间的数量关系为.
(2)
【深入探究】操作二:如图2、将
°;②线段EF , BE , DF之间的数量关系为.
(2)
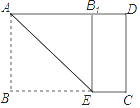
【深入探究】操作二:如图2、将 沿EF所在直线折叠,使点C落在正方形ABCD的内部,点C的对应点为N,将纸片展平,连接NE、NF.同学们在折纸的过程中发现,当点E的位置不同时,点N的位置也不同,当点E在BC边上某一位置时(点E不与点B,C重合),点N恰好落在折痕AE上,此时AM交NF于点P,如图3所示.
沿EF所在直线折叠,使点C落在正方形ABCD的内部,点C的对应点为N,将纸片展平,连接NE、NF.同学们在折纸的过程中发现,当点E的位置不同时,点N的位置也不同,当点E在BC边上某一位置时(点E不与点B,C重合),点N恰好落在折痕AE上,此时AM交NF于点P,如图3所示.
小明通过观察图形,测量并猜想,得到结论 , 请证明该结论是否成立,并说明理由.
(3)
【拓展应用】
, 请证明该结论是否成立,并说明理由.
(3)
【拓展应用】
小明通过观察图形,测量并猜想,得到结论
若正方形纸片ABCD的边长为3,当点N落在折痕AE上时,求出线段BE的长.
【考点】
正方形的判定与性质;
翻折变换(折叠问题);