某数学兴趣小组活动，准备将一张三角形纸片 (如图) 进行如下操作，并进行猜想和证明．

1. 某数学兴趣小组活动，准备将一张三角形纸片 (如图) 进行如下操作，并进行猜想和证明．

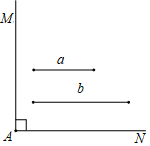
(1) 用三角板分别取 $\text{[math]}$ 的中点 $\text{[math]}$ ，连接 $\text{[math]}$ ，画 $\text{[math]}$ 于点 $\text{[math]}$ ；

(2) 用 (1) 中所画的三块图形经过旋转或平移拼出一个四边形(无缝隙无重叠)，并用三角板画出示意图；

(3) 请判断 (2) 中所拼的四边形的形状，并说明理由．

【考点】

矩形的判定; 作图﹣旋转; 利用旋转设计图案; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

作图题困难

求作：矩形ABCD，使得矩形ABCD的两条边长分别等于线段a和线段b．

下面是小东设计的尺规作图过程．

作法：如图，

①以点A为圆心，b为半径作弧，交AN于点B；

②以点A为圆心，a为半径作弧，交AM于点D；

③分别以点B、点D为圆心，a、b长为半径作弧，两弧交于∠MAN内部的点C；

④分别连接BC，DC．

所以四边形ABCD就是所求作的矩形．

根据小东设计的尺规作图过程，

证明：

∵AB＝；AD＝；

∴四边形ABCD是平行四边形．

∵∠MAN＝90°；

∴四边形ABCD是矩形（填依据）．

作图题普通

①在图中作出△ABC关于点O对称的△A₁B₁C₁（不写作法，但需在图中标注相应字母）；

②已知点A、B的坐标分别为A（﹣4，4）、B（﹣3，1），求点C₁的坐标．

作图题普通

⑴以O为旋转中心，将△ABC顺时针旋转90°得到△A₁B₁C₁；

⑵以O为对称中心，作出△ABC关于点O的中心对称图形ΔA₂B₂C₂；

作图题普通