1.
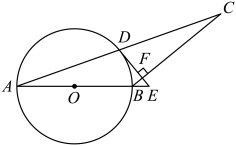
如图, 是
是 的外接圆,
的外接圆, 为
为 的直径,
的直径, 的平分线
的平分线 交
交 于点
于点 , 过点D作
, 过点D作 , 交
, 交 的延长线于点E .
的延长线于点E .

(1)
求证:直线 是
是 的切线;
(2)
求证:
的切线;
(2)
求证: ;
(3)
若
;
(3)
若 , 求
, 求 的长(用含m , n的代数式表示).
的长(用含m , n的代数式表示).
【考点】
等腰三角形的判定与性质;
圆周角定理;
相似三角形的判定与性质;
能力提升
真题演练