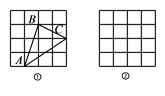1.
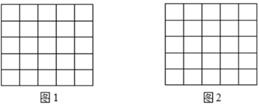
图 1、图 2、图 3 均是  的正方形网格, 每个小正方形的边长均为 1 , 其顶点称为格点,
的正方形网格, 每个小正方形的边长均为 1 , 其顶点称为格点,  的顶点均在格点上. 只用无刻度的直尺, 在给定的网格中, 按下列要求作图,保留作图痕迹.
的顶点均在格点上. 只用无刻度的直尺, 在给定的网格中, 按下列要求作图,保留作图痕迹.

(1)
网格中  的形状是.
(2)
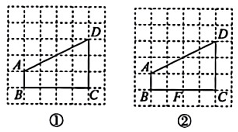
在图 1 中确定一点
的形状是.
(2)
在图 1 中确定一点  , 连结
, 连结  , 使
, 使  与
与  全等.
(3)
在图 2 中
全等.
(3)
在图 2 中  的边
的边  上确定一点
上确定一点  , 连结
, 连结  , 使
, 使  .
(4)
在图 3 中
.
(4)
在图 3 中  的边
的边  上确定一点
上确定一点  , 在边
, 在边  上确定一点
上确定一点  , 连结
, 连结  , 使
, 使 
 , 且相似比为
, 且相似比为  .
.
【考点】
三角形全等的判定;
勾股定理;
勾股定理的逆定理;
相似三角形的判定;
三角形的中位线定理;
能力提升