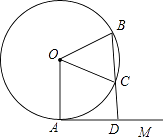1.
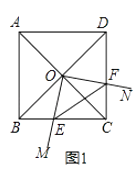
如图, 在  中,
中,  , 点
, 点  是斜边
是斜边  上一点, 以
上一点, 以  为圆心的
为圆心的  分别与
分别与  相切于点
相切于点  .
.

(1)
当  时, 求
时, 求  的半径.
(2)
设
的半径.
(2)
设  的半径为
的半径为  , 求
, 求  与
与  之间的函数关系式.
之间的函数关系式.
【考点】
正方形的判定与性质;
切线的性质;
正切的概念;
能力提升