1.
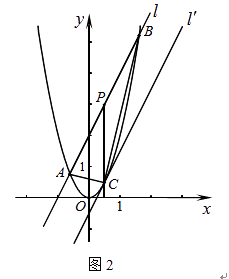
如图，抛物线y＝ax2+bx+c与x轴相交于A（
， 0）、B（
， 0）两点，与y轴交于点C（0，
），连接BC ， 抛物线顶点M ．
(1)
求抛物线的解析式；
(2)
把抛物线y＝ax2+bx+c在x轴下方图象沿x轴翻折得到新图象．平移直线BC得函数y＝mx+n ， 当直线y＝mx+n与新图象有四个公共点时，求n的取值范围；
(3)
平移直线BC ， 使它过点M ， 交x轴于点D ， 在x轴上取点E（
， 0）连接EM ， 求∠BEM﹣∠BDM的度数．
【考点】
一元二次方程根的判别式及应用;
二次函数图象的几何变换;
解直角三角形;
二次函数与一次函数的综合应用;
一次函数图象的平移变换;
