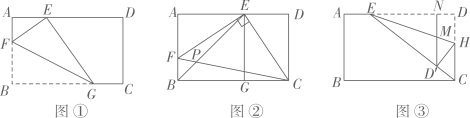
综合探究【问题情境】综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．如图1是一张矩形纸片ABCD ，其中，．【操作发现】

0 返回出卷网首页

1. 综合探究

【问题情境】综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．如图1是一张矩形纸片ABCD ，其中 $\text{[math]}$ ， $\text{[math]}$ ．

【操作发现】

(1) 奋进小组先将图1中的矩形纸片ABCD沿直线BD折叠，使得点C落在点E处，BE交AD于点P ，得到图2，他们发现 $\text{[math]}$ ．请你证明这个结论；

(2) 创新小组将图1中的矩形纸片折叠，使得点A落在对角线BD上，记为点G ，折痕为BF ，得到图3，则 $\text{[math]}$ ；

(3) 【实践探究】

希望小组在创新小组操作的基础上，将图3中的纸片展开，然后提出一个问题：将矩形纸片ABCD沿直线AH折叠，使得点B落在对角线BD上的点 $\text{[math]}$ 处，然后将纸片展平，如图4所示，折痕AH交BF于点M ，交BD于点N ，试判断 $\text{[math]}$ 的形状；

(4) 请你根据希望小组的操作，求点G到AD的距离．

【考点】

勾股定理; 翻折变换（折叠问题）; 相似三角形的判定与性质; 三角形全等的判定-AAS; 四边形的综合;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 某“数学学习兴趣小组”成员在复习《图形的变化》时，对下面的图形背景产生了浓厚的兴趣，并尝试运用由“特殊到一般”的思想进行了探究：

(1) 【问题背景】如图1，正方形ABCD中，点E为AB边上一点，连接DE，过点E作EF⊥DE交BC边于点F，将△ADE沿直线DE折叠后，点A落在点 $\text{[math]}$ 处，当∠BEF＝25°，则∠FE $\text{[math]}$ ＝°．

(2) 【特例探究】如图2，连接DF，当点 $\text{[math]}$ 恰好落在DF上时，求证：AE＝2 $\text{[math]}$ F．

(3) 【深入探究】若把正方形ABCD改成矩形ABCD，且AD＝mAB，其他条件不变，他们发现AE与 $\text{[math]}$ F之间也存在着一定的数量关系，请直接写出AE与 $\text{[math]}$ F之间的数量关系式．

(4) 【拓展探究】若把正方形ABCD改成菱形ABCD，且∠B＝60°，∠DEF＝120°，其他条件不变，他们发现AE与 $\text{[math]}$ F之间也存在着一定的数量关系，请直接写出AE与A′F之间的数量关系式．

实践探究题困难

2. 在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 如图①，将矩形 $\text{[math]}$ 折叠，使顶点 $\text{[math]}$ 落在边 $\text{[math]}$ 上的点 $\text{[math]}$ 处，折痕的一端点 $\text{[math]}$ 在边 $\text{[math]}$ 上．当折痕的另一端点 $\text{[math]}$ 在边 $\text{[math]}$ 上，且 $\text{[math]}$ 时， $\text{[math]}$ 的度数为；

(2) 如图②，将矩形 $\text{[math]}$ 折叠，使顶点 $\text{[math]}$ 落在边 $\text{[math]}$ 上的点 $\text{[math]}$ 处，折痕的一端点 $\text{[math]}$ 在边 $\text{[math]}$ 上，另一端点为矩形 $\text{[math]}$ 的顶点 $\text{[math]}$ ．将 $\text{[math]}$ 折叠后重新展开，连接 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交线段 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，与 $\text{[math]}$ 交于点 $\text{[math]}$ ．求 $\text{[math]}$ 长；

(3) 如图③，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 折叠，连接 $\text{[math]}$ ，折叠后点 $\text{[math]}$ 落在 $\text{[math]}$ 边上的点 $\text{[math]}$ 处，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，与 $\text{[math]}$ 交于点 $\text{[math]}$ ，且 $\text{[math]}$ ．求 $\text{[math]}$ 的面积．

实践探究题困难

3. 问题情境：如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线 $\text{[math]}$ 如图 $\text{[math]}$ ，将 $\text{[math]}$ 的两个顶点 $\text{[math]}$ ， $\text{[math]}$ 分别沿 $\text{[math]}$ ， $\text{[math]}$ 折叠后均与点 $\text{[math]}$ 重合，折痕分别交 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 猜想证明：如图 $\text{[math]}$ ，试判断四边形 $\text{[math]}$ 的形状，并说明理由；

(2) 问题解决：如图 $\text{[math]}$ ，将图 $\text{[math]}$ 中左侧折叠的三角形展开后，重新沿 $\text{[math]}$ 折叠，使得顶点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，折痕分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对应线段交 $\text{[math]}$ 于点 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积．

实践探究题困难