1.
已知在正方形ABCD中，
， 点P在边CD上，
， 点Q是射线AP上的一个动点，过点Q作AB的平行线交射线BC于点M，点R在直线BC上，使RQ始终与射线AP垂直．
(1)
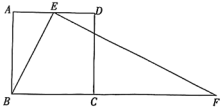
如图1，当点R与点C重合时，求PQ的长；
(2)
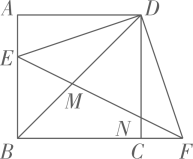
如图2，试探索：
的值是否随点Q的运动而发生变化？若有变化，请说明理由并求出变化规律；若没有变化，请求出它的比值；
(3)
如图3，当点Q在线段AP上，设
， 请用含x的式子表示RM．
【考点】
勾股定理;
正方形的性质;
相似三角形的判定与性质;
锐角三角函数的定义;
