1.
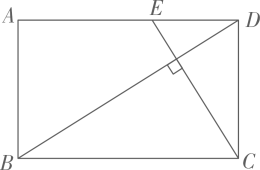
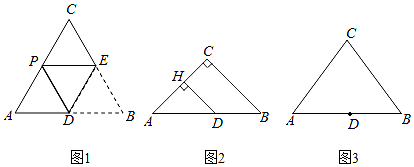
如图1,平面上,四边形 中,
中, ,
,  ,
,  ,
,  ,
,  , 点M在
, 点M在 边上,且
边上,且 . 点P沿折线
. 点P沿折线 以1个单位速度向终点C运动,点
以1个单位速度向终点C运动,点 是点A关于直线
是点A关于直线 的对称点,连接
的对称点,连接 , 设点P在该折线上运动的时间为
, 设点P在该折线上运动的时间为 .
.

(1)
直接写出线段 的长;
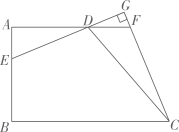
(2)
如图2,连接
的长;
(2)
如图2,连接 .
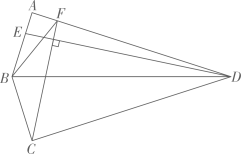
(3)
当
.
(3)
当 时,请直接写出点
时,请直接写出点 到直线
到直线 的距离(用含t的式子表示).
的距离(用含t的式子表示).
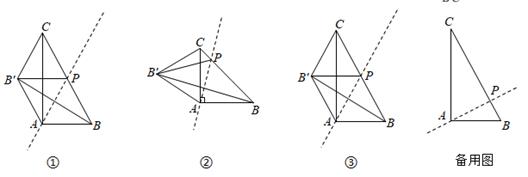
①求的度数,并直接写出当
、M、A共线时t的值;
②若点P到的距离为1,求
的值;
【考点】
翻折变换(折叠问题);
相似三角形的判定与性质;
解直角三角形;
能力提升
真题演练