已知如图，四边形ABDC坐标为A（9，0），B（5，1），C（5，4），D（2，4）．

0 返回出卷网首页

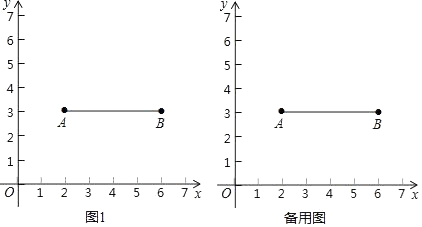
1. 已知如图，四边形ABDC坐标为A（9，0），B（5，1），C（5，4），D（2，4）．

(1) 请在边长为1的小正方形组成的网格中建立平面直角坐标系，然后在平面直角坐标系中画出四边形ABDC．

(2) 求四边形ABDC的面积．

【考点】

坐标与图形性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．根据所给定义解决下列问题：

(1) 若已知点D（1，2）、E（﹣2，1）、F（0，6），则这3点的“矩面积”=．

(2) 若D（1，2）、E（﹣2，1）、F（0，t）三点的“矩面积”为18，求点F的坐标．

综合题普通

2. 在平面直角坐标系xOy中，点A的坐标为（1，0），P是第一象限内任意一点，连接PO，PA，若∠POA=m°，∠PAO=n°，则我们把（m°，n°）叫做点P 的“双角坐标”．例如，点（1，1）的“双角坐标”为（45°，90°）．

(1) 点（ $\text{[math]}$ ， $\text{[math]}$ ）的“双角坐标”为；

(2) 若点P到x轴的距离为 $\text{[math]}$ ，则m+n的最小值为．

综合题普通

3. 如图，在平面直角坐标系中，给出如下定义：已知点A（2，3），点B（6，3），连接AB．如果线段AB上有一个点与点P的距离不大于1，那么称点P是线段AB的“环绕点”．

(1) 已知点C（3，1.5），D（4，3.5），E（1，3），则是线段AB的“环绕点”的点是；

(2) 已知点P（m，n）在反比例函数y= $\text{[math]}$ 的图象上，且点P是线段AB的“环绕点”，求出点P的横坐标m的取值范围；

(3) 已知⊙M上有一点P是线段AB的“环绕点”，且点M（4，1），求⊙M的半径r的取值范围．

综合题普通