如图，在△ABC中，∠C=150°，AC=4，tanB= ．

0 返回出卷网首页

1. 如图，在△ABC中，∠C=150°，AC=4，tanB= $\text{[math]}$ ．

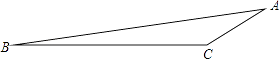
(1) 求BC的长；

(2) 利用此图形求tan15°的值（精确到0.1，参考数据： $\text{[math]}$ =1.4， $\text{[math]}$ =1.7， $\text{[math]}$ =2.2）

【考点】

锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 某游乐场部分平面图如图所示，C、E、A在同一直线上，D、E、B在同一直线上，测得A处与E处的距离为80 米，C处与D处的距离为34米，∠C=90°，∠BAE=30°．（ $\text{[math]}$ ≈1.4， $\text{[math]}$ ≈1.7）

(1) 求旋转木马E处到出口B处的距离；

(2) 求海洋球D处到出口B处的距离（结果保留整数）．

综合题普通

2. 在8×8的正方形网格中，有一个Rt△AOB，点O是直角顶点，点O、A、B分别在网格中小正方形的顶点上，请按照下面要求在所给的网格中画图．

(1) 在图1中，将△AOB先向右平移3个单位，再向上平移2个单位，得到△A₁O₁B₁ ，画出平移后的△A₁O₁B₁；（其中点A、O、B的对应点分别为点A₁ ， O₁ ， B₁）

(2) 在图2中，△AOB与△A₂O₂B₂是关于点P对称的图形，画出△A₂O₂B₂ ，连接BA₂ ，并直接写出tan∠A₂BO的值．（其中A，O，B的对应点分别为点A₂ ， O₂ ， B₂）

综合题普通

3. 如图，△ABC中，AB=AC=13，BD⊥AC于点D，sinA= $\text{[math]}$ ．

(1) 求BD的长.

(2) 求tanC的值．

综合题普通