1.
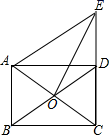
如图,在 中,
中, ,
,  ,
,  , 点
, 点 从点
从点 出发沿
出发沿 方向以每秒
方向以每秒 个单位长度的速度向点
个单位长度的速度向点 匀速运动,同时点
匀速运动,同时点 从点
从点 出发沿
出发沿 方向以每秒
方向以每秒 个单位长度的速度向点
个单位长度的速度向点 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点 ,
,  运动的时间是
运动的时间是 秒,过点
秒,过点 作
作 于点
于点 , 连接
, 连接 ,
,  .
.

(1)
求证:四边形 是平行四边形;
(2)
当
是平行四边形;
(2)
当 为何值时,
为何值时, 是等边三角形?说明理由;
(3)
当
是等边三角形?说明理由;
(3)
当 为何值时,
为何值时, 为直角三角形?(请直接写出
为直角三角形?(请直接写出 的值)
的值)
【考点】
等边三角形的性质;
含30°角的直角三角形;
勾股定理;
平行四边形的判定与性质;
三角形-动点问题;