在△ABC中，CA=CB，在△AED中，DA=DE，点D，E分别在CA，AB上．

0 返回出卷网首页

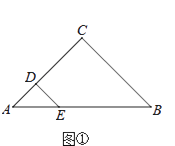
1. 在△ABC中，CA=CB，在△AED中，DA=DE，点D，E分别在CA，AB上．

(1) 如图①，若∠ACB=∠ADE=90°，则CD与BE的数量关系是；

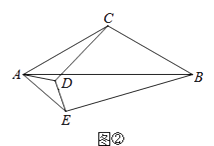
(2) 若∠ACB=∠ADE=120°，将△AED绕点A旋转至如图②所示的位置，则CD与BE的数量关系是；，

(3) 若∠ACB=∠ADE=2α（0°＜α＜90°），将△AED绕点A旋转至如图③所示的位置，探究线段CD与BE的数量关系，并加以证明（用含α的式子表示）．

【考点】

相似三角形的判定与性质; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 于D ， $\text{[math]}$ 于E ， $\text{[math]}$ 交 $\text{[math]}$ 于F

(1) 求证： $\text{[math]}$ ；

(2) 求 $\text{[math]}$ （用含m的代数式表示）；

(3) 当 $\text{[math]}$ 时，求 $\text{[math]}$ 的最大值．

综合题困难

2. 已知，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是斜边 $\text{[math]}$ 的中点， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，连结 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ；

(2) 当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；

(3) 在（2）的条件下，求 $\text{[math]}$ 的值．

综合题普通

3. 在Rt△ABC中，∠ACB＝90°，BC＝30，AB＝50．点P是AB边上任意一点，直线PE⊥AB，与边AC相交于E．点M在线段AP上，点N在线段BP上，EM＝EN，tan∠EMP＝ $\text{[math]}$

(1) 如图1，当点E与点C重合时，求PM的长；

(2) 如图2，当点E在边AC上时，点E不与点A、C重合，设AP＝x，BN＝y，用含x的代数式表示PN，并求y关于x的函数关系式，且写出函数的自变量取值范围；

(3) 如图2，若△AME∽△ENB（△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应），求AP的长．

综合题普通