某植物园有一块足够大的空地，其中有一堵长为6米的墙，现准备用20米的篱笆围两间矩形花圃，中间用篱笆隔开．小俊设计了如图所示的两种方案：方案甲中AD的长不超过墙长；方案乙中AD的长大于墙长．

0 返回出卷网首页

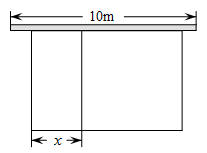
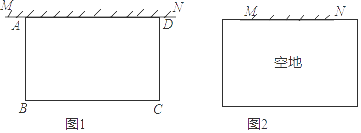
1. 某植物园有一块足够大的空地，其中有一堵长为6米的墙，现准备用20米的篱笆围两间矩形花圃，中间用篱笆隔开．小俊设计了如图所示的两种方案：方案甲中AD的长不超过墙长；方案乙中AD的长大于墙长．

(1) 若按方案甲施工，且围成面积为25平方米的花圃，则AD的长是多少米？

(2) 按哪种方案施工，可以围成的矩形花圃的面积最大？最大面积是多少？

【考点】

一元二次方程的应用-几何问题; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为 $\text{[math]}$ ），另外三面用棚栏围成，中间再用栅栏把它分成两个面积比为1：2的矩形（如图）.已知栅栏的总长度为24m，设较小矩形的宽为 $\text{[math]}$ .

(1) 若矩形养殖场的总面积为 $\text{[math]}$ ，求此时 $\text{[math]}$ 的值.

(2) 当 $\text{[math]}$ 为多少时，矩形养殖场的总面积最大？最大值为多少？

解答题普通

2. 如图，计划利用长为a米的篱笆，再借助外墙围成一个矩形栅栏，设矩形 $\text{[math]}$ 的边 $\text{[math]}$ 长为x米，面积为y平方米.

(1) 若 $\text{[math]}$ ，墙长为 $\text{[math]}$ 米，求出y与x之间的关系，并指出x的取值范围；

(2) 在（1）的条件下，矩形 $\text{[math]}$ 的面积能达到 $\text{[math]}$ 平方米吗？说明理由；

(3) 当x与a满足什么关系时，栅栏围出的面积最大？最大值是多少？

解答题普通

3. 某居民小区要在一块一边靠墙（墙长15米）的空地上修建一个矩形花园 $\text{[math]}$ ，花园的一边靠墙，另三边用总长40米的栅栏围成（如图所示）．若设花园的 $\text{[math]}$ 边长为x米，花园的面积为y平方米．

(1) 求y与x之间的函数关系式，并写出自变量x的取值范围；

(2) 满足条件的花园面积能否达到150平方米？若能，请求出x的值；若不能，请说明理由；

(3) 当x是多少时，矩形场地面积y最大？最大面积是多少？

解答题困难