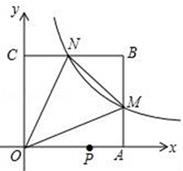
已知点A（1，2）、点 B在双曲线y= （x＞0）上，过B作BC⊥x轴于点C，如图，P是y轴上一点，

0 返回出卷网首页

1. 已知点A（1，2）、点 B在双曲线y= $\text{[math]}$ （x＞0）上，过B作BC⊥x轴于点C，如图，P是y轴上一点，

(1) 求k的值及△PBC的面积；

(2) 设点M（x₁ ， y₁）、N（x₂ ， y₂）（x₂＞x₁＞0）是双曲线y= $\text{[math]}$ （x＞0）上的任意两点，s= $\text{[math]}$ ，t= $\text{[math]}$ ，试判断s与t的大小关系，并说明理由．

【考点】

反比例函数系数k的几何意义; 待定系数法求反比例函数解析式; 反比例函数图象上点的坐标特征;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在平面直角坐标系中，反比例函数y＝ $\text{[math]}$ （x＞0）的图象与边长是6的正方形OABC的两边AB ， BC分别相交于M ， N两点．

(1) 若点M是AB边的中点，求反比例函数y＝ $\text{[math]}$ 的解析式和点N的坐标；

(2) 若AM＝2，求直线MN的解析式及△OMN的面积．

综合题困难

2. 如图，四边形OP₁A₁B₁、A₁P₂A₂B₂、A₂P₃A₃B₃、…、A_n_﹣₁P_nA_nB_n都是正方形，对角线OA₁、A₁A₂、A₂A₃、…、A_n_﹣₁A_n都在y轴上（n≥1的整数），点P₁（x₁ ， y₁），点P₂（x₂ ， y₂），…，P_n（x_n ， y_n）在反比例函数y= $\text{[math]}$ （x＞0）的图象上，并已知B₁（﹣1，1）．

(1) 求反比例函数y= $\text{[math]}$ 的解析式；

(2) 求点P₂和点P₃的坐标；

(3) 由（1）、（2）的结果或规律试猜想并直接写出：△P_nB_nO的面积为，点P_n的坐标为（用含n的式子表示）．

综合题困难

3. 如图1，点A（m ， 6），B（6，1）在反比例函数图象上，作直线AB ，连接OA、OB ．

(1) 求反比例函数的表达式和m的值；

(2) 求△AOB的面积；

(3) 如图2，E是线段AB上一点，作AD⊥x轴于点D ，过点E作x轴的垂线，交反比例函数图象于点F ，若EF＝ $\text{[math]}$ AD ，求出点E的坐标．

综合题困难