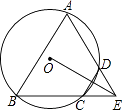
1.
如图,圆O的内接四边形ABCD中,AD是⊙O的直径,BC=CD .

(1)
如图1,求证:∠ABC=90°+∠BAC;
(2)
如图2,OH⊥BC , 垂足是H , 求证:AC=2OH;
(3)
如图3,在(2)的条件下,作CE⊥AD交⊙于点E , 垂足是F , 连接EO并延长交AB于点M , 若OH=4,OF•AM=10,求BM的长.
【考点】
垂径定理;
圆内接四边形的性质;
直角三角形的性质;
相似三角形的性质-对应边;
圆与四边形的综合;