1.
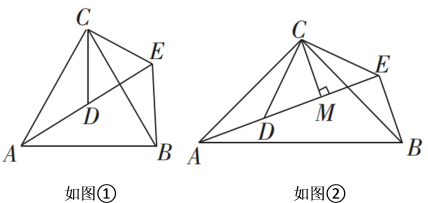
亮亮学习《平行四边形》以后，利用身边的工具进行了如下操作与探究：如图1，在边长为
的正方形纸板ABCD上，放置了一个三角板PEQ，作射线AC，使直角顶点E在射线AC上运动，EP始终经过点D，EQ交BC于点F．
依照上面操作，点E运动到如图2位置时，连接DE，EF，过点F作FG⊥EF于点F，过点D作DG⊥FG于点G，于是得到矩形DEFG，通过证明它的一组邻边相等，易证矩形DEFG为正方形，亮亮又作了如下思考，请你帮他完成以下问题：
(1)
若点E运动到线段AC的延长线上时，以上结论还成立吗？若成立，应该怎样画图，证明呢？若不成立，理由是什么？
(2)
在（1）的情况下，若连接CG，CG﹣CE的值是否为定值？若是，结果是多少（直接写出结果即可）？若不是，理由是什么？
【考点】
平行线的性质;
矩形的性质;
正方形的判定与性质;
三角形全等的判定-SAS;
