1.
【问题背景】如图①，在四边形
中，
和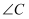
称为它的对角，若这个四边形满足：
， 则这个四边形叫做为“对角互补四边形”．
【问题解决】
(1)
若四边形是“对角互补四边形”，且
， 求
的度数；
(2)
如图②，
， 
平分
， A是射线
上一动点，C是射线
上的动点，且四边形
是“对角互补四边形”．
①若是等腰三角形，求
的度数；
②若 ， 若
， 求
的长（用含m、n的代数式表示）．
【考点】
角平分线的性质;
等腰三角形的判定与性质;
勾股定理;
多边形内角与外角;
