1.
在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 , 并且原多边形上的任一点
, 并且原多边形上的任一点 , 它的对应点
, 它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 , 记为
, 记为 , 如果是顺时针旋转一个角度
, 如果是顺时针旋转一个角度 , 则记为
, 则记为 , 这种经过位似和旋转的图形变换叫做旋转相似变换,其中点
, 这种经过位似和旋转的图形变换叫做旋转相似变换,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)
填空:
(2)
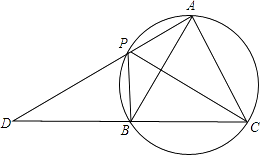
如图3, 经过
经过 得到
得到 , 又将
, 又将 经过
经过 得到
得到 , 连接
, 连接 ,
,  , 求证:四边形
, 求证:四边形 是平行四边形.
(3)
如图4,在
是平行四边形.
(3)
如图4,在 中,
中, ,
,  ,
,  , 若
, 若 经过(2)中的变换得到的四边形
经过(2)中的变换得到的四边形 恰好是正方形时,则
恰好是正方形时,则 的长为___________.
的长为___________.
①如图1,将以点
为旋转相似中心,放大为原来的2倍,再逆时针旋转
, 得到
, 这个旋转相似变换记为
(___________,___________);

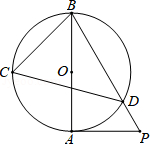
②如图2,是边长为
的等边三角形,将它作旋转相似变换
, 得到
, 则线段
的长为___________
;



【考点】
等边三角形的判定与性质;
圆周角定理;
解直角三角形;
旋转的性质;
相似三角形的性质-对应边;