1.
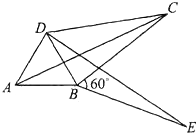
定义:菱形一边的中点与它所在边的对边的两个端点连线所形成的折线,叫做菱形的折中线.例如,如图1,在菱形 中,E是
中,E是 的中点,连接
的中点,连接 , 则折线
, 则折线 叫做菱形
叫做菱形 的折中线,折线
的折中线,折线 的长叫做折中线的长.
的长叫做折中线的长.
已知,在菱形中,
, E是
的中点,连接
,
.

(1)
如图1,若 ,
,  , 求折中线
, 求折中线 的长;
(2)
如图2,若
的长;
(2)
如图2,若 , 请探究折中线
, 请探究折中线 的长与菱形的边长a之间满足的等量关系式,并说明理由;
(3)
若
的长与菱形的边长a之间满足的等量关系式,并说明理由;
(3)
若 , 且折中线
, 且折中线 中的
中的 或
或 与菱形
与菱形 的一条对角线相等,求折中线
的一条对角线相等,求折中线 的长.
的长.
【考点】
等边三角形的判定与性质;
勾股定理;
菱形的性质;
相似三角形的判定;
相似三角形的性质-对应边;