1.
如果三角形的两个内角a与β满足2a+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)
基础巩固:
(2)
尝试应用:
(3)
拓展提高:
若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B=°;
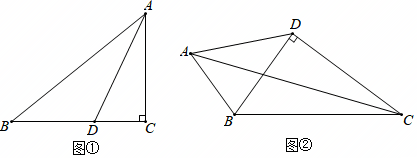
如图①,在Rt△ABC中,∠ACB=90°,∠BAC=50°.
①若AD是∠BAC的平分线,判断△ABD是否是“准互余三角形” ▲ (是、否);
②在边BC上存在点E(异于点D),使得△ABE也是“准互余三角形”,求此时∠EAC的度数;
如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD , ∠ABD=2∠BCD , 且△ABC是“准互余三角形”,求对角线AC的长.
【考点】
勾股定理;
翻折变换(折叠问题);
直角三角形的性质;
角平分线的概念;