1.
1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”.
(1)
下面是该问题的一种常见的解决方法,分两种情况讨论,请补充以下推理过程:
(2)
如图3,在 中,三个内角均小于
中,三个内角均小于 , 且
, 且 ,
,  ,
,  , 若P为
, 若P为 的“费马点”,求
的“费马点”,求 的值;
(3)
如图4,设村庄A,B,C的连线构成一个三角形,且已知
的值;
(3)
如图4,设村庄A,B,C的连线构成一个三角形,且已知 ,
,  ,
,  . 现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为1万元
. 现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为1万元 , 1万元
, 1万元 ,
,  万元
万元 , 则总的铺设成本最少是万元.
, 则总的铺设成本最少是万元.
①当的三个内角均小于
时,
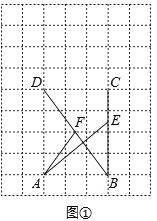
如图1,将绕点C顺时针旋转
得到
, 连接
,




∵绕点C顺时针旋转
得到
∴
,
∴为三角形,∴
∵∴
∴
由几何公理:可得:
∴当B,P, ,
在同一条直线上时,
取最小值,
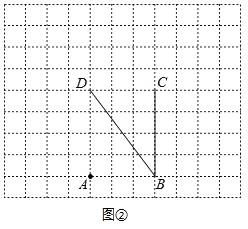
如图2,最小值为
, 此时的P点为该三角形的“费马点”,且有
°.
②当有一个内角大于或等于
时,“费马点”为该三角形的某个顶点,证明略.
【考点】
勾股定理;
轴对称的应用-最短距离问题;
费马点模型;
能力提升